Si hay un número mágico en el arte ese es el número áureo, dorado o de oro. A este número irracional se le han atribuido peculiaridades divinas y estéticas perfectas. Descubierto en la antigüedad podemos ver su uso desde en la Gran pirámide de Gizeh, pasando por el Partenón hasta llegar a la misma música de Debussy.
El número dorado
El número es un número irracional que se representa principalmente por la letra griega φ/ Φ (Phi) en honor al escultor griego Fidias. También se representa con la letra griega Tau (Τ/τ), cuando se refiere al concepto sección (áurea) y la letra griega alpha minúscula.
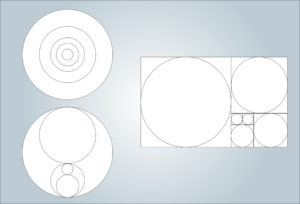
Este número fue descubierto en la antigüedad, no como una expresión aritmética, sino como relación o proporción entre dos segmentos de una recta, es decir, una construcción geométrica. Esta proporción se encuentra tanto en algunas figuras geométricas como en la naturaleza: en las nervaduras de las hojas de algunos árboles, en el grosor de las ramas, en el caparazón de un caracol, en los flósculos de los girasoles, etc. Una de sus propiedades aritméticas más curiosas es que su cuadrado (Φ2 = 2,61803398874988…) y su inverso (1/Φ = 0,61803398874988…) tienen las mismas infinitas cifras decimales.
Asimismo, se atribuye un carácter estético a los objetos cuyas medidas guardan la proporción áurea. Algunos incluso creen que posee una importancia mística. A lo largo de la historia, se ha atribuido su inclusión en el diseño de diversas obras de arquitectura y otras artes, aunque algunos de estos casos han sido cuestionados por los estudiosos de las matemáticas y el arte.
Algunos autores sugieren que el número áureo se encuentra como proporción en varias estelas de Babilonia y Asiria de alrededor de 2000 a. C. Sin embargo, no existe documentación histórica que indique que el número áureo fuera utilizado conscientemente.
El primero en hacer un estudio formal del número áureo fue Euclides (c. 300-265 a. C.), quien lo definió como irracional y constató sus características: «Se dice que una recta ha sido cortada en extrema y media razón cuando la recta entera es al segmento mayor como el segmento mayor es al segmento menor».
Antes de él lo había citado Platón. Platón consideró que los números irracionales, descubiertos por los pitagóricos, eran de particular importancia y la llave de la física d
el cosmos. Esta opinión tuvo una gran influencia en muchos filósofos y matemáticos posteriores, en particular los neoplatónicos.
A pesar de lo discutible de su conocimiento sobre el número áureo, Platón se ocupó de estudiar el origen y la estructura del cosmos, cosa que intentó usando los cinco sólidos platónicos, construidos y estudiados por Teeteto. En particular, combinó la idea de Empédocles sobre la existencia de cuatro elementos básicos de la materia, con la teoría atómica de Demócrito. Para Platón, cada uno de los sólidos correspondía a una de las partículas que conformaban cada uno de los elementos: la tierra estaba asociada al cubo, el fuego al tetraedro, el aire al octaedro, el agua al icosaedro, y finalmente el Universo como un todo, estaba asociado con el dodecaedro.
En 1509 el matemático y teólogo italiano Luca Pacioli publicó “De Divina Proportione” (La Divina Proporci). En su valoración, estima que el número áureo es divino. Para ello esgrima cinco razones: La unicidad, la trinidad, la omnipresencia, la inconmensurabilidad y la quinta esencia. Estas características las comparten Dios y el número áureo.
Alberto Durero publicó “Instrucción sobre la medida con regla y compás de figuras planas y sólidas” en 1525. En él, describe cómo trazar con regla y compás la espiral áurea basada en la sección áurea y se conoce como “espiral de Durero”.
También el astrónomo Johannes Kepler (1571-1630) se refirió al número áureo en términos grandiosos en su ”Mysterium Cosmographicum” (El misterio cósmico).: “La geometría tiene dos grandes tesoros: uno es el teorema de Pitágoras; el otro, la división de una línea entre el extremo y su proporcional. El primero lo podemos comparar a una medida de plata; el segundo lo debemos denominar una joya preciosa.
Pero quien le atribuyó el adjetivo áureo fue el matemático alemán Martin Ohm, en la segunda edición de 1835 de su libro Die Reine Elementar Matematik (Las matemáticas puras elementales). Ohm escribe en una nota al pie: «Uno también acostumbra llamar a esta división de una línea arbitraria en dos partes como éstas la sección dorada».
Y es que a principios del siglo XIX, todo el mundo lo conocía ya por el número o sección áureos. En los textos de matemáticas que trataban el tema, el símbolo habitual para representar el número áureo fue τ, del griego τομή, que significa ‘corte o sección’. Sin embargo, la moderna denominación Φ o φ la efectuó en 1900 el matemático Mark Barr en honor a Fidias, ya que ésta era la primera letra de su nombre escrito en griego (Φειδίας). Este honor se le concedió a Fidias por el máximo valor estético atribuido a sus esculturas, propiedad que ya por entonces se le atribuía también al número áureo.
La proporción áurea en el arte
Aunque ya Herodoto hablaba de las relaciones en la forma de la Gran Pirámide de Gizeh con la proporción áurea, es la cultura clásica griega la que lo muestra de forma excelsa.
La relación entre las partes, el techo y las columnas del Partenón, en Atenas, siguen esta proporción. Y es que la proporción áurea tiene que ver con la relación entre el círculo y el rectángulo. No fue hasta 1837 cuando se dieron cuenta de las correcciones ópticas en el Partenón. El templo tiene tres vistas principales. Si sus columnas, planos y ángulos fueran rectos, el ojo humano lo vería más ancho arriba que en la base, sus columnas se percibirían inclinadas hacia afuera y la línea que fundamenta el techo sobre las columna
s se vería aparentemente más altos que el centro. En definitiva, los arquitectos eran conscientes de la deformación que el ojo humano genera y lo construyeron compensando esa ilusión.
Para compensarlo, aplicaron el número áureo. Así las columnas exteriores, en ambos lados del frente, están inclinadas hacia adentro en un ángulo de 2,65 segundos de arco, mientras que las que están en el medio tienen una inclinación de 2,61 segundos de arco. La línea que formarían los dinteles entre columnas y que constituye la base del triángulo que corona el edificio, en realidad es un ángulo de 2,64 segundos de arco con el vértice más elevado que los extremos. Como consecuencia el edificio se percibe paralelo, uniforme y recto.
Durante el primer cuarto del siglo XX, Jay Hambidge, de la Universidad de Yale, se inspiró en un pasaje del Teeteto de Platón para estudiar las proporciones relativas de las superficies. Estudios como los del doctor Fechner han demostrado que la percepción de la belleza radica en la proporción áurea. Aquello que siga esa proporción o se acerque se percibirá como más bello y perfecto.
Esta noción de belleza y perfección es aplicable a estructuras arquitectónicas, pinturas, partituras musicales, fractales y personas.
Entre los ejemplos, podemos encontrar “Leda atómica”, de Salvador Dalí. En las estructuras y tiempos de las películas «El acorazado Potemkin» e «Iván el Terrible» de Serguéi Eisenstein. En los violines, la ubicación de las efes o eses (los “oídos” u orificios en la tapa) se relaciona con el número áureo. El número áureo aparece en las relaciones entre altura y ancho de los objetos y personas que aparecen en las obras de Miguel Ángel, Durero y Leonardo Da Vinci, entre otros.
En las estructuras formales de las sonatas de Wolfgang Amadeus Mozart, en la Quinta Sinfonía de Ludwig van Beethoven, en obras de Franz Schubert y Claude Debussy, consciente o de forma incosciente.
Los ejemplos son números, por citar alguno más significativo, el arte Póvera fue un movimiento artístico italiano de los años 1960 en el que muchas de cuyas obras se basan en esta sucesión.
